110.字符串迁移
题目描述
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列:
- 序列中第一个字符串是 beginStr。
- 序列中最后一个字符串是 endStr。
- 每次转换只能改变一个字符。
- 转换过程中的中间字符串必须是字典 strList 中的字符串,且strList里的每个字符串只用使用一次。
给你两个字符串 beginStr 和 endStr 和一个字典 strList,找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列,返回 0。
输入描述
第一行包含一个整数 N,表示字典 strList 中的字符串数量。 第二行包含两个字符串,用空格隔开,分别代表 beginStr 和 endStr。 后续 N 行,每行一个字符串,代表 strList 中的字符串。
输出描述
输出一个整数,代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列,则输出 0。
输入示例
6
abc def
efc
dbc
ebc
dec
dfc
yhn
输出示例
4
提示信息
从 startStr 到 endStr,在 strList 中最短的路径为 abc -> dbc -> dec -> def,所以输出结果为 4
数据范围:
2 <= N <= 500
解题思路
import java.util.*;
class Main {
static int ans = 0;
static Map<String, Set<String>> map = new HashMap<>();
// 判断时s2是否是s1的下一个
static boolean canConverted(String s1, String s2) {
if (s1.length() != s2.length()) {
return false;
}
int diff = 0, n = s1.length();
for (int i = 0; i < n; i++) {
if (s1.charAt(i) != s2.charAt(i)) {
diff++;
if (diff > 1) {
return false;
}
}
}
return diff == 1;
}
static void bfs(String beginStr, String endStr, Map<String, List<String>> graph) {
Queue<String> que = new LinkedList<>();
// 存储到达 str 的距离
Map<String, Integer> dist = new HashMap<>();
que.offer(beginStr);
dist.put(beginStr, 1); // 路径长度从 1 开始计
while (!que.isEmpty()) {
String cur = que.poll();
int d = dist.get(cur);
if (cur.equals(endStr)) {
ans = d;
return;
}
for (String next : graph.get(cur)) {
// dist 没有才放入
if (!dist.containsKey(next)) {
dist.put(next, d + 1);
que.offer(next);
}
}
}
}
static Map<String, List<String>> constructGraph(List<String> strList) {
Map<String, List<String>> graph = new HashMap<>();
for (String s : strList) {
graph.put(s, new ArrayList<>());
}
for (int i = 0; i < strList.size(); i++) {
for (int j = i + 1; j < strList.size(); j++) {
String a = strList.get(i);
String b = strList.get(j);
if (canConverted(a, b)) {
graph.get(a).add(b);
graph.get(b).add(a);
}
}
}
return graph;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
String beginStr = in.next();
String endStr = in.next();
List<String> strList = new ArrayList<>();
strList.add(beginStr);
strList.add(endStr);
for (int i = 0; i < n; i++) {
strList.add(in.next());
}
in.close();
Map<String, List<String>> graph = constructGraph(strList);
bfs(beginStr, endStr, graph);
System.out.println(ans);
}
}
105.有向图的完全联通
题目描述
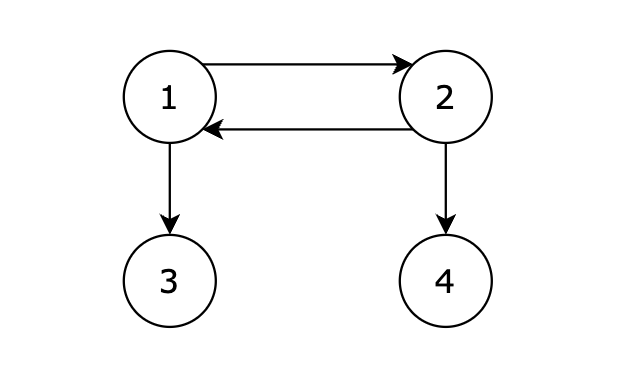
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,…,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入描述
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
输出描述
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入示例
4 4
1 2
2 1
1 3
2 4
输出示例
1
提示信息
从 1 号节点可以到达任意节点,输出 1。
数据范围:
1 <= N <= 100;
1 <= K <= 2000。
解题思路
import java.util.*;
class Main {
static void dfs(int[][] graph, int from, boolean[] visited){
if (visited[from]) {
return;
}
visited[from] = true;
for (int to = 0; to < graph.length; to++) {
if (graph[from][to] == 1) {
dfs(graph, to, visited);
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(), k = in.nextInt();
int[][] graph = new int[n][n];
for (int i = 0; i < k; i++) {
int s = in.nextInt() - 1, t = in.nextInt() - 1;
graph[s][t] = 1;
}
in.close();
boolean[] visited = new boolean[n];
dfs(graph, 0, visited);
boolean ans = true;
// 查看所有节点是否都被访问
for (boolean v : visited) {
ans &= v;
}
System.out.println(ans ? 1 : -1);
}
}
106.海岸线计算
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿,假设组成岛屿的陆地边长都为 1,请计算海岸线,即:岛屿的周长。岛屿内部没有水域。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的周长。
输入示例
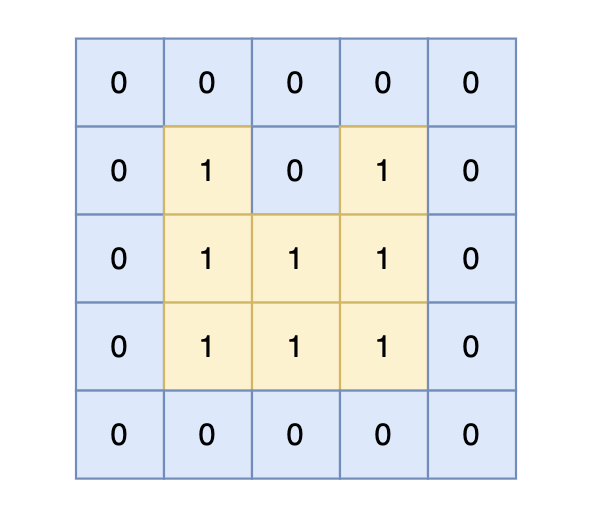
5 5
0 0 0 0 0
0 1 0 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0
输出示例
14
提示信息
岛屿的周长为 14。
数据范围:
1 <= M, N <= 50。
解题思路
要求海岸线的周长,即求每个岛屿的 上下左右 有几个是临海的,临海则为海岸线。
import java.util.*;
class Main {
static int dirs[][] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
static int perimeter = 0;
static void dfs(int[][] martix, int x, int y) {
for (int[] dir : dirs) {
int nextX = x + dir[0];
int nextY = y + dir[1];
// 下一次遍历的是边界或者是 0 则令周长加 1
if (nextX < 0 || nextX >= martix.length
|| nextY < 0 || nextY >= martix[0].length
|| martix[nextX][nextY] == 0) {
perimeter++;
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(), m = in.nextInt();
int[][] martix = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
martix[i][j] = in.nextInt();
}
}
in.close();
boolean[][] visited = new boolean[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (martix[i][j] == 1) {
dfs(martix, i, j);
}
}
}
System.out.println(perimeter);
}
}


评论