Floyd 算法精讲
97.小明逛公园
题目描述
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
输入描述
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
输出描述
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
输入示例
7 3
2 3 4
3 6 6
4 7 8
2
2 3
3 4
输出示例
4
-1
提示信息
从 2 到 3 的路径长度为 4,3 到 4 之间并没有道路。
1 <= N, M, Q <= 1000.
1 <= w <= 10000.
解题思路
import java.util.*;
public class Main {
static final int INF = 0x3f3f3f3f;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int M = in.nextInt();
int[][] dist = new int[N + 1][N + 1];
// 初始化为 INF
for (int i = 1; i <= N; i++) {
Arrays.fill(dist[i], INF);
dist[i][i] = 0;
}
// 读入无向边
for (int i = 0; i < M; i++) {
int u = in.nextInt();
int v = in.nextInt();
int w = in.nextInt();
dist[u][v] = w;
dist[v][u] = w;
}
// Floyd
for (int k = 1; k <= N; k++) { // 枚举中转点
for (int i = 1; i <= N; i++) { // 枚举起点
if (dist[i][k] == INF) continue; // 小剪枝
for (int j = 1; j <= N; j++) { // 枚举终点
if (dist[k][j] == INF) continue;
if (dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
int Q = in.nextInt();
while (Q-- > 0) {
int start = in.nextInt();
int end = in.nextInt();
if (dist[start][end] == INF) {
System.out.println(-1);
} else {
System.out.println(dist[start][end]);
}
}
in.close();
}
}
A * 算法精讲 (A star算法)
127.骑士的攻击
题目描述
在象棋中,马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
输入描述
第一行包含一个整数 n,表示测试用例的数量,1 <= n <= 100。
接下来的 n 行,每行包含四个整数 a1, a2, b1, b2,分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。
输出描述
输出共 n 行,每行输出一个整数,表示骑士从起点到目标点的最短路径长度。
输入示例
6
5 2 5 4
1 1 2 2
1 1 8 8
1 1 8 7
2 1 3 3
4 6 4 6
输出示例
2
4
6
5
1
0
提示信息
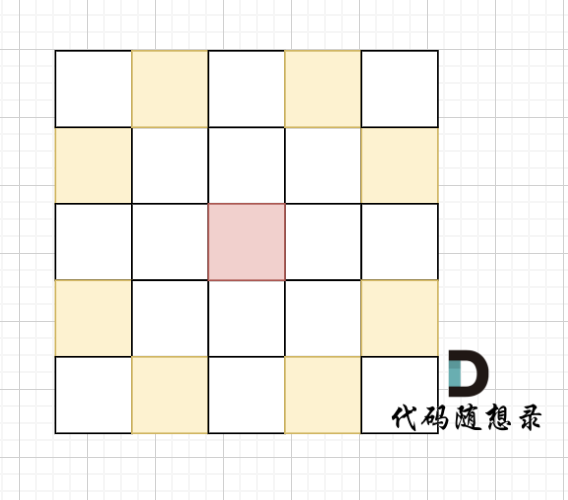
骑士移动规则如图,红色是起始位置,黄色是骑士可以走的地方。
解题思路
import java.util.*;
public class Main {
static final int MAX = 1000;
static final int INF = 1_000_000_000;
static final int[][] dirs = {
{1, 2}, {1, -2}, {2, 1}, {2, -1},
{-1, 2}, {-1, -2}, {-2, 1}, {-2, -1}
};
// dist[dx][dy] = 从 (0,0) 到 (dx,dy) 的最短骑士步数
static int[][] dist = new int[MAX + 1][MAX + 1];
public static void main(String[] args) {
// 一次性预处理
preprocess();
Scanner in = new Scanner(System.in);
int T = in.nextInt();
while (T-- > 0) {
int x1 = in.nextInt();
int y1 = in.nextInt();
int x2 = in.nextInt();
int y2 = in.nextInt();
int dx = Math.abs(x1 - x2);
int dy = Math.abs(y1 - y2);
// 利用对称性:保证 dx >= dy
if (dx < dy) {
int tmp = dx; dx = dy; dy = tmp;
}
System.out.println(dist[dx][dy]);
}
}
// 从 (0,0) 开始,一次性 BFS 预处理所有距离
static void preprocess() {
for (int i = 0; i <= MAX; i++) {
Arrays.fill(dist[i], INF);
}
ArrayDeque<int[]> q = new ArrayDeque<>();
dist[0][0] = 0;
q.offer(new int[]{0, 0});
while (!q.isEmpty()) {
int[] cur = q.poll();
int x = cur[0], y = cur[1];
for (int k = 0; k < 8; k++) {
int[] dir = dirs[k];
int nx = x + dir[0];
int ny = y + dir[1];
if (nx < 0 || ny < 0 || nx > MAX || ny > MAX) continue;
if (dist[nx][ny] != INF) continue;
dist[nx][ny] = dist[x][y] + 1;
q.offer(new int[]{nx, ny});
}
}
}
}


评论