dijkstra(堆优化版)精讲
47.参加科学大会(第六期模拟笔试)
题目描述
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
输入描述
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
输出描述
输出一个整数,代表小明从起点到终点所花费的最小时间。
输入示例
7 9
1 2 1
1 3 4
2 3 2
2 4 5
3 4 2
4 5 3
2 6 4
5 7 4
6 7 9
输出示例
12
提示信息
能够到达的情况:
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
不能到达的情况:
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
数据范围:
1 <= N <= 500;
1 <= M <= 5000;
解题思路
import java.util.*;
public class Main {
static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
// int[0]: 下一个节点名 int[1]:到达int[0]的权值
List<int[]>[] graph = new ArrayList[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
int s = scanner.nextInt();
int e = scanner.nextInt();
int v = scanner.nextInt();
graph[s].add(new int[]{e, v});
}
int[] dist = new int[n + 1];
Arrays.fill(dist, INF);
dist[1] = 0;
// 构造优先队列
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
// 加入初始状态
pq.offer(new int[]{1, 0});
while (!pq.isEmpty()) {
int[] cur = pq.poll();
int node = cur[0];
int val = cur[1];
// 剪枝
if (val > dist[node]) {
continue;
}
// 更新 dist 数组
for (int[] edge : graph[node]) {
int nextNode = edge[0];
int nextVal = edge[1];
// 从起点到达新的节点的距离 大于 从原点 -> 中转点 -> 新节点的距离;更新到新节点距离
if (dist[nextNode] > dist[node] + nextVal) {
dist[nextNode] = dist[node] + nextVal;
pq.offer(edge);
}
}
}
System.out.println(dist[n] == INF ? -1 : dist[n]);
}
}
Bellman_ford 算法精讲
94.城市间货物运输 I
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v (单向图)。
输出描述
如果能够从城市 1 到连通到城市 n, 请输出一个整数,表示运输成本。如果该整数是负数,则表示实现了盈利。如果从城市 1 没有路径可达城市 n,请输出 “unconnected”。
输入示例
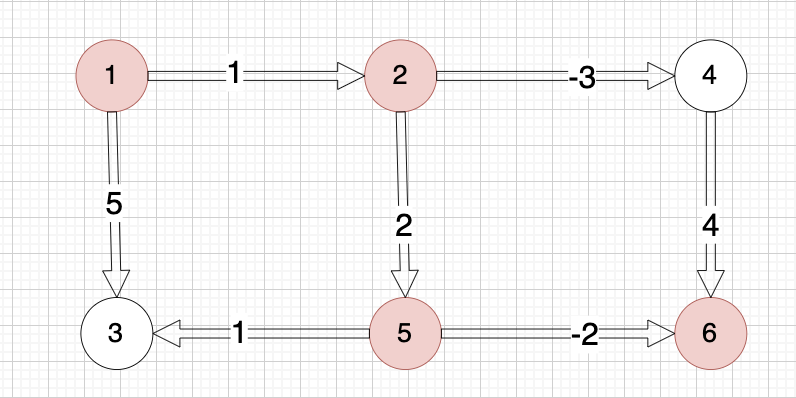
6 7
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5
输出示例
1
提示信息
示例中最佳路径是从 1 -> 2 -> 5 -> 6,路上的权值分别为 1 2 -2,最终的最低运输成本为 1 + 2 + (-2) = 1。
示例 2:
4 2
1 2 -1
3 4 -1在此示例中,无法找到一条路径从 1 通往 4,所以此时应该输出 “unconnected”。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
解题思路
用边表存图:(from, to, w)。
dist[1] = 0,其他初始化为 INF。
做 n-1 轮:每轮把所有边都拿出来尝试一次松弛。
最后看 dist[n]:
- 如果还是
INF,说明不可达 → 输出"unconnected" - 否则输出
dist[n](可能为负,表示盈利)
import java.util.*;
public class Main {
static class Edge {
int from, to, w;
Edge(int from, int to, int w) {
this.from = from;
this.to = to;
this.w = w;
}
}
// 用一个足够大的数当作无穷大,避免溢出
static final int INF = 0x3f3f3f3f;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
List<Edge> edges = new ArrayList<>();
for (int i = 0; i < m; i++) {
int s = in.nextInt();
int t = in.nextInt();
int v = in.nextInt();
edges.add(new Edge(s, t, v));
}
int[] dist = new int[n + 1];
Arrays.fill(dist, INF);
dist[1] = 0; // 起点
// Bellman-Ford 核心:最多 n-1 轮松弛
for (int k = 1; k <= n - 1; k++) {
boolean updated = false;
for (Edge e : edges) {
if (dist[e.from] != INF && dist[e.to] > dist[e.from] + e.w) {
dist[e.to] = dist[e.from] + e.w;
updated = true;
}
}
// 一轮都没更新,说明已经收敛,可以提前结束
if (!updated) break;
}
if (dist[n] == INF) {
System.out.println("unconnected");
} else {
System.out.println(dist[n]);
}
}
}
Bellman_ford 队列优化算法(又名SPFA)
题目如上
解题思路
“只让那些刚被更新过的点继续往外扩散,不用每一轮都扫所有边。”
做法:
- 图换成邻接表:
graph[u] = (v, w)列表。 dist[1] = 0,起点入队。- 队列 BFS 一样弹点
u,对u的所有出边(u -> v, w)做松弛:- 如果
dist[v]被更新变小,并且 v 不在队列里,就把 v 入队。
- 如果
- 队列空了说明再也没有可以更新的点,结束。
import java.util.*;
public class Main {
static class Edge {
int to, w;
Edge(int to, int w) {
this.to = to;
this.w = w;
}
}
static final int INF = 0x3f3f3f3f;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
// 邻接表
List<Edge>[] graph = new ArrayList[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
int s = in.nextInt();
int t = in.nextInt();
int v = in.nextInt();
graph[s].add(new Edge(t, v));
}
int[] dist = new int[n + 1];
Arrays.fill(dist, INF);
dist[1] = 0;
boolean[] inQueue = new boolean[n + 1];
Queue<Integer> q = new ArrayDeque<>();
q.offer(1);
inQueue[1] = true;
while (!q.isEmpty()) {
int u = q.poll();
inQueue[u] = false;
for (Edge e : graph[u]) {
int v = e.to;
int w = e.w;
if (dist[u] != INF && dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
if (!inQueue[v]) {
q.offer(v);
inQueue[v] = true;
}
}
}
}
if (dist[n] == INF) {
System.out.println("unconnected");
} else {
System.out.println(dist[n]);
}
}
}

评论