101.孤岛的总面积
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被陆地单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
1
提示信息
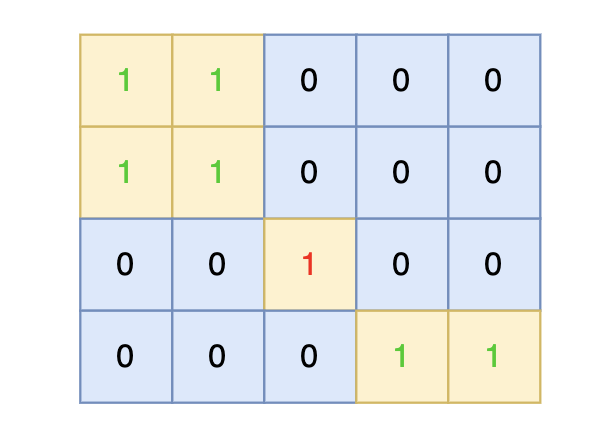
在矩阵中心部分的岛屿,因为没有任何一个单元格接触到矩阵边缘,所以该岛屿属于孤岛,总面积为 1。
数据范围:
1 <= M, N <= 50。
解题思路
将边缘陆地以及和它相邻的陆地假定为海洋,然后求陆地的数量
import java.util.*;
class Main {
public static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public static void dfs(int[][] martix, int x, int y) {
martix[x][y] = 0;
for (int i = 0; i < 4; i++) {
int nextX = x + dir[i][0];
int nextY = y + dir[i][1];
if (nextX < 0 || nextX >= martix.length
|| nextY < 0 || nextY >= martix[0].length) {
continue;
}
if (martix[nextX][nextY] == 1) {
dfs(martix, nextX, nextY);
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int m = in.nextInt(), n = in.nextInt();
int[][] martix = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
martix[i][j] = in.nextInt();
}
}
in.close();
for (int i = 0; i < m; i++) {
if (martix[i][0] == 1) {
dfs(martix, i, 0);
}
if (martix[i][n - 1] == 1) {
dfs(martix, i, n - 1);
}
}
for (int j = 0; j < n; j++) {
if (martix[0][j] == 1) {
dfs(martix, 0, j);
}
if (martix[m - 1][j] == 1) {
dfs(martix, m - 1, j);
}
}
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (martix[i][j] == 1) {
ans++;
}
}
}
System.out.println(ans);
}
}
102.沉没孤岛
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要将所有孤岛“沉没”,即将孤岛中的所有陆地单元格(1)转变为水域单元格(0)。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。
之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出将孤岛“沉没”之后的岛屿矩阵。 注意:每个元素后面都有一个空格
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
1 1 0 0 0
1 1 0 0 0
0 0 0 0 0
0 0 0 1 1
提示信息
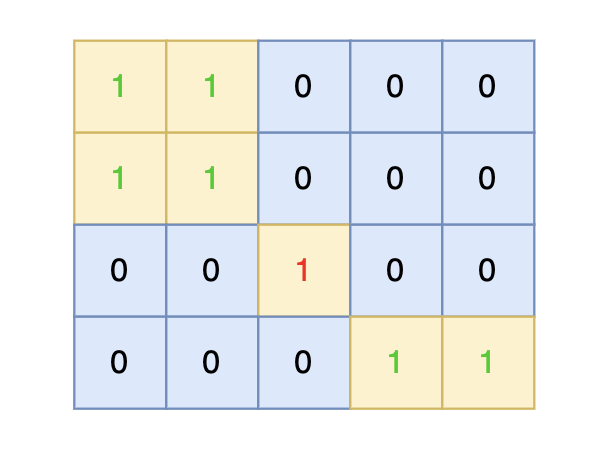
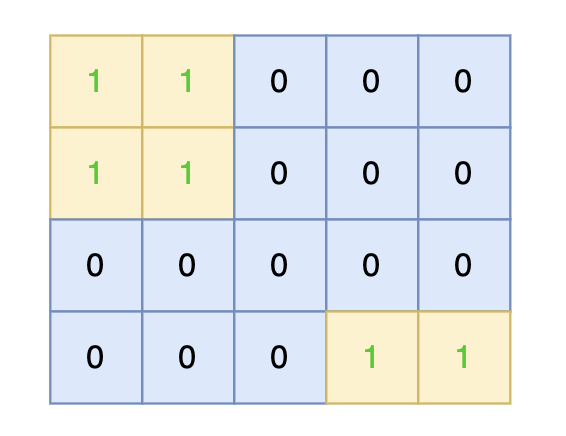
将孤岛沉没。
数据范围:
1 <= M, N <= 50。
解题思路
上一题基础上,将和边缘陆地有关的置为-1,后面再将为陆地的沉底(置为0),标记的置回为陆地
import java.util.*;
class Main {
public static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public static void dfs(int[][] martix, int x, int y) {
martix[x][y] = -1;
for (int i = 0; i < 4; i++) {
int nextX = x + dir[i][0];
int nextY = y + dir[i][1];
if (nextX < 0 || nextX >= martix.length
|| nextY < 0 || nextY >= martix[0].length) {
continue;
}
if (martix[nextX][nextY] == 1) {
dfs(martix, nextX, nextY);
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int m = in.nextInt(), n = in.nextInt();
int[][] martix = new int[m][n];
int sum = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
martix[i][j] = in.nextInt();
sum += martix[i][j];
}
}
in.close();
for (int i = 0; i < m; i++) {
if (martix[i][0] == 1) {
dfs(martix, i, 0);
}
if (martix[i][n - 1] == 1) {
dfs(martix, i, n - 1);
}
}
for (int j = 0; j < n; j++) {
if (martix[0][j] == 1) {
dfs(martix, 0, j);
}
if (martix[m - 1][j] == 1) {
dfs(martix, m - 1, j);
}
}
int cnt = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (martix[i][j] == 1) {
martix[i][j] = 0;
} else if (martix[i][j] == -1) {
martix[i][j] = 1;
}
System.out.print(martix[i][j] + " ");
}
System.out.println();
}
}
}
103.高山流水
题目描述
现有一个 N × M 的矩阵,每个单元格包含一个数值,这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界,而矩阵的右边界和下边界被视为第二组边界。
矩阵模拟了一个地形,当雨水落在上面时,水会根据地形的倾斜向低处流动,但只能从较高或等高的地点流向较低或等高并且相邻(上下左右方向)的地点。我们的目标是确定那些单元格,从这些单元格出发的水可以达到第一组边界和第二组边界。
输入描述
第一行包含两个整数 N 和 M,分别表示矩阵的行数和列数。
后续 N 行,每行包含 M 个整数,表示矩阵中的每个单元格的高度。
输出描述
输出共有多行,每行输出两个整数,用一个空格隔开,表示可达第一组边界和第二组边界的单元格的坐标,输出顺序任意。
输入示例
5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1
输出示例
0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1
提示信息
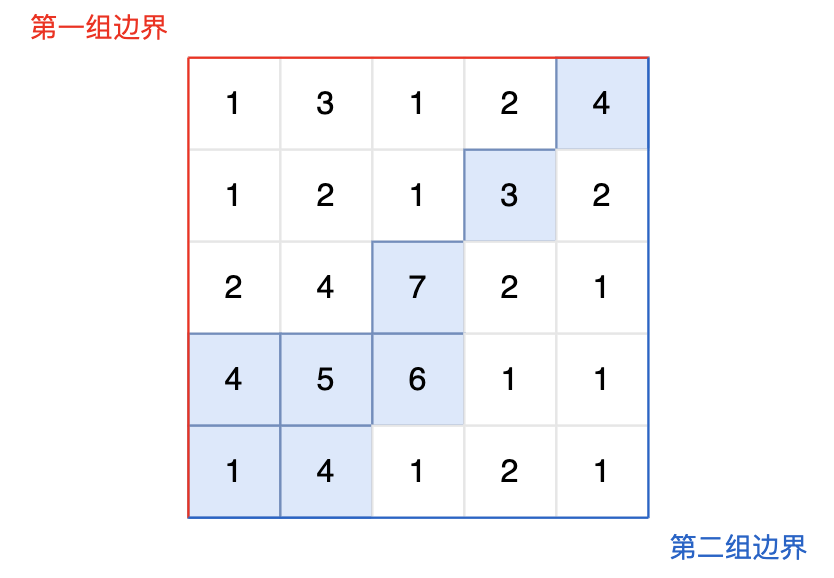
图中的蓝色方块上的雨水既能流向第一组边界,也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
数据范围:
1 <= M, N <= 100。
解题思路
import java.util.*;
class Main {
public static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public static void dfs(int[][] martix, boolean[][] visited, int x, int y, int prefH) {
if (x < 0 || x >= martix.length
|| y < 0 || y >= martix[0].length
|| visited[x][y]) {
return;
}
if (martix[x][y] < prefH) {
return;
}
visited[x][y] = true;
dfs(martix, visited, x + 1, y, martix[x][y]);
dfs(martix, visited, x - 1, y, martix[x][y]);
dfs(martix, visited, x, y + 1, martix[x][y]);
dfs(martix, visited, x, y - 1, martix[x][y]);
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int m = in.nextInt(), n = in.nextInt();
int[][] martix = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
martix[i][j] = in.nextInt();
}
}
in.close();
boolean[][] first = new boolean[m][n];
boolean[][] second = new boolean[m][n];
for (int i = 0; i < m; i++) {
dfs(martix, second, i, 0, Integer.MIN_VALUE);
dfs(martix, first, i, n - 1, Integer.MIN_VALUE);
}
for (int j = 0; j < n; j++) {
dfs(martix, second, 0, j, Integer.MIN_VALUE);
dfs(martix, first, m - 1, j, Integer.MIN_VALUE);
}
List<int[]> ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (first[i][j] && second[i][j]) {
ans.add(new int[]{i, j});
}
}
}
for (int[] item : ans) {
System.out.println(item[0] + " " + item[1]);
}
}
}
104.建造最大岛屿
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,你最多可以将矩阵中的一格水变为一块陆地,在执行了此操作之后,矩阵中最大的岛屿面积是多少。
岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示最大的岛屿面积。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
6
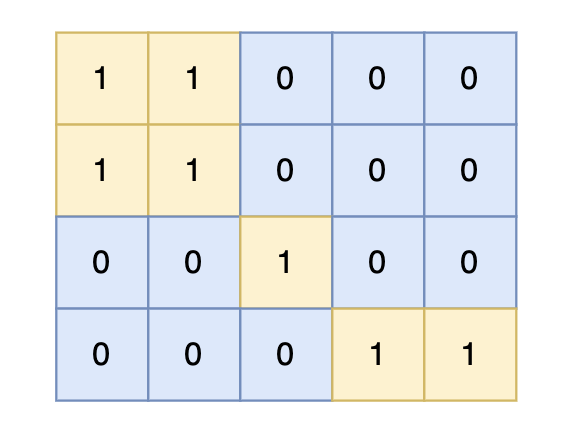
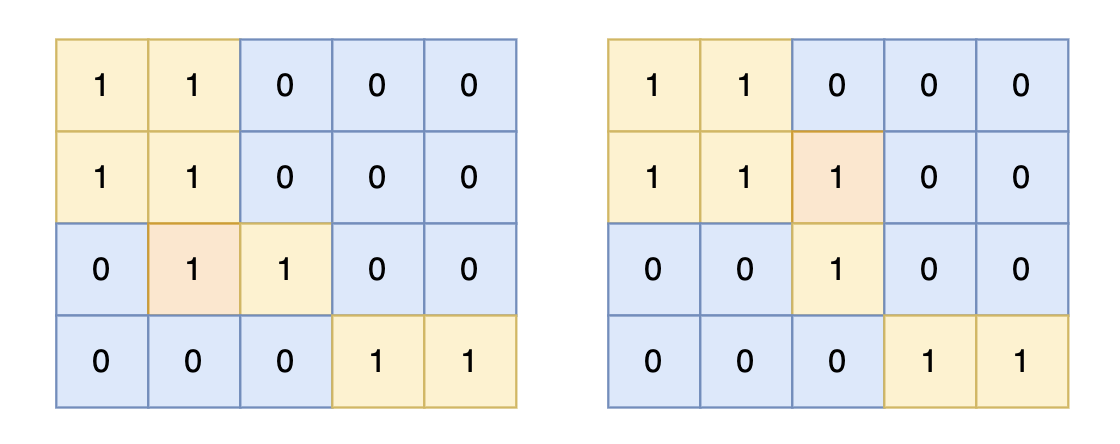
提示信息
对于上面的案例,有两个位置可将 0 变成 1,使得岛屿的面积最大,即 6。
数据范围:
1 <= M, N <= 50。
解题思路
将已有的岛屿进行编号,并将对应的面积保存在map中。然后求每个0(海洋)上下左右的岛屿编号对应的面积,再与之相加求最大
import java.util.*;
class Main {
static int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
// 记录岛屿的最大面积
static int ans = 0;
// 记录每个编号的岛屿面积
static Map<Integer, Integer> map = new HashMap<>();
static void dfs(int[][] martix, boolean[][] visited, int x, int y, int mark) {
visited[x][y] = true;
martix[x][y] = mark;
map.put(mark, map.getOrDefault(mark, 0) + 1);
ans = Math.max(map.get(mark), ans);
for (int[] dir : dirs) {
int nextX = x + dir[0];
int nextY = y + dir[1];
if (nextX < 0 || nextX >= martix.length
|| nextY < 0 || nextY >= martix[0].length) {
continue;
}
if (!visited[nextX][nextY] && martix[nextX][nextY] == 1) {
dfs(martix, visited, nextX, nextY, mark);
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int m = in.nextInt(), n = in.nextInt();
int[][] martix = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
martix[i][j] = in.nextInt();
}
}
in.close();
boolean[][] visited = new boolean[m][n];
int mark = 2;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (!visited[i][j] && martix[i][j] == 1) {
dfs(martix, visited, i, j, mark);
mark++;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (martix[i][j] == 0) {
int area = 1;
// 统计上下左右的岛屿编号
Set<Integer> set = new HashSet<>();
for (int[] dir : dirs) {
int nextX = i + dir[0];
int nextY = j + dir[1];
if (nextX < 0 || nextX >= m
|| nextY < 0 || nextY >= n
|| martix[nextX][nextY] == 0) {
continue;
}
set.add(martix[nextX][nextY]);
}
for (Integer key : set) {
area += map.get(key);
}
ans = Math.max(area, ans);
}
}
}
System.out.println(ans);
}
}


评论