图论 part05

107.寻找存在的路线

题目描述

给定一个包含 n 个节点的无向图中，节点编号从 1 到 n （含 1 和 n ）。

你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。

输入描述

第一行包含两个正整数 N 和 M，N 代表节点的个数，M 代表边的个数。

后续 M 行，每行两个正整数 s 和 t，代表从节点 s 与节点 t 之间有一条边。

最后一行包含两个正整数，代表起始节点 source 和目标节点 destination。

输出描述

输出一个整数，代表是否存在从节点 source 到节点 destination 的路径。如果存在，输出 1；否则，输出 0。

输入示例

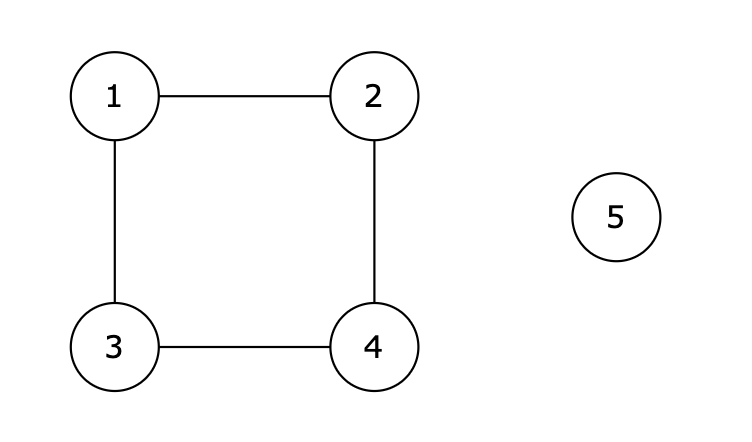
5 4
1 2
1 3
2 4
3 4
1 4

输出示例

1

提示信息

数据范围：

1 <= M, N <= 100。

解题思路

深度搜索

这种方法需要构造邻接矩阵，如果邻接矩阵过大。则查找起来很费时。

import java.util.*;
class Main {
    static int n;
    static int[][] graph;
    static int source;
    static int destination;

    public static void init() {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        int m = in.nextInt();
        graph = new int[n][n];
        for (int i = 0; i < m; i++) {
            int s = in.nextInt() - 1;
            int t = in.nextInt() - 1;
            graph[s][t] = 1;
            graph[t][s] = 1;
        }

        source = in.nextInt() - 1;
        destination = in.nextInt() - 1;
        in.close();
    }
    public static void dfs(int from, boolean[] visited) {
        visited[from] = true;
        for (int to = 0; to < n; to++) {
            if (!visited[to] && graph[from][to] == 1) {
                dfs(to, visited);
            }
        }
    }
    public static void main(String[] args) {
        init(); 
        boolean[] visited = new boolean[n];
        dfs(source, visited);
        System.out.println(visited[destination] ? 1 : 0);
    }
}

并查集

import java.util.*;
 
public class Main{
    public static void main(String[] args) {
        int N, M;
        Scanner in = new Scanner(System.in);
        N = in.nextInt();
        M = in.nextInt();
        DisJoint disJoint = new DisJoint(N + 1);

        for (int i = 0; i < M; ++i) {
            disJoint.join(in.nextInt(), in.nextInt());
        }

        if(disJoint.isSame(in.nextInt(), in.nextInt())) {
            System.out.println("1");
        } else {
            System.out.println("0");
        }
    }
 
}

//并查集
class DisJoint{
    // i 的老大是谁, 默认是它自己
    private int[] father;
 
    public DisJoint(int n) {
        father = new int[n];
        for (int i = 0; i < n; ++i){
            father[i] = i;
        }
    }

    // 找老大
    public int find(int n) {
        // 路径优化。先执行find(father[n])、再赋值、然后返回括号的值
        return n == father[n] ? n : (father[n] = find(father[n]));
    }

    // 吸纳新成员
    public void join (int n, int m) {
        n = find(n);
        m = find(m);
        if (n == m) return;
        father[m] = n;
    }

    // 查看是否同属于一个老大
    public boolean isSame(int n, int m){
        n = find(n);
        m = find(m);
        return n == m;
    }
 
}