1456. 定长子串中元音的最大数目
题目描述
给你字符串 s 和整数 k 。
请返回字符串 s 中长度为 k 的单个子字符串中可能包含的最大元音字母数。
英文中的 元音字母 为(a, e, i, o, u)。
示例
输入:s = "leetcode", k = 3
输出:2
解释:"lee"、"eet" 和 "ode" 都包含 2 个元音字母。
解题思路
class Solution {
Set<Character> vowel = new HashSet<>(Arrays.asList('a','e','i','o','u'));
public int maxVowels(String s, int k) {
int ans = 0;
int cur = 0;
for (int right = 0; right < s.length(); right++) {
if (vowel.contains(s.charAt(right))) {
cur++;
}
int left = right - k + 1;
// 还未形成有效窗口,继续遍历
if (left < 0) {
continue;
}
// 形成有效窗口,开始运算
ans = Math.max(cur, ans);
// 为下一次准备
if (ans == k) break;
if (vowel.contains(s.charAt(left))) {
cur--;
}
}
return ans;
}
}
643. 子数组最大平均数 I
题目描述
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
任何误差小于 10-5 的答案都将被视为正确答案。
示例
输入:nums = [1,12,-5,-6,50,3], k = 4
输出:12.75
解释:最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
解题思路
class Solution {
public double findMaxAverage(int[] nums, int k) {
int right = 0;
int left = 0;
int maxS = Integer.MIN_VALUE;
int sum = 0;
while (right < nums.length) {
sum += nums[right++];
if (right - left == k) {
maxS = Math.max(sum, maxS);
sum -= nums[left++];
}
}
// 先求最大和,最后在除k
return (double) maxS / k;
}
}
1343. 大小为 K 且平均值大于等于阈值的子数组数目
题目描述
给你一个整数数组 arr 和两个整数 k 和 threshold 。
请你返回长度为 k 且平均值大于等于 threshold 的子数组数目。
示例
输入:arr = [2,2,2,2,5,5,5,8], k = 3, threshold = 4
输出:3
解释:子数组 [2,5,5],[5,5,5] 和 [5,5,8] 的平均值分别为 4,5 和 6 。其他长度为 3 的子数组的平均值都小于 4 (threshold 的值)。
解题思路
class Solution {
public int numOfSubarrays(int[] arr, int k, int threshold) {
int left = 0, right = 0;
int sum = 0;
int ans = 0;
threshold *= k; // 转换为和为目标值
while (right < arr.length) {
sum += arr[right++];
if (right - left == k) {
if (sum >= threshold) {
ans++;
}
sum -= arr[left++];
}
}
return ans;
}
}
2090. 半径为 k 的子数组平均值
题目描述
给你一个下标从 0 开始的数组 nums ,数组中有 n 个整数,另给你一个整数 k 。
半径为 k 的子数组平均值 是指:nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值,即下标在 i - k 和 i + k 范围(含 i - k 和 i + k)内所有元素的平均值。如果在下标 i 前或后不足 k 个元素,那么 半径为 k 的子数组平均值 是 -1 。
构建并返回一个长度为 n 的数组 avgs ,其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。
x 个元素的 平均值 是 x 个元素相加之和除以 x ,此时使用截断式 整数除法 ,即需要去掉结果的小数部分。
- 例如,四个元素
2、3、1和5的平均值是(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75,截断后得到2。
示例
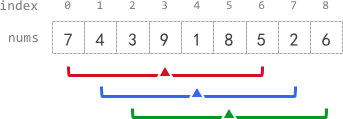
输入:nums = [7,4,3,9,1,8,5,2,6], k = 3
输出:[-1,-1,-1,5,4,4,-1,-1,-1]
解释:
- avg[0]、avg[1] 和 avg[2] 是 -1 ,因为在这几个下标前的元素数量都不足 k 个。
- 中心为下标 3 且半径为 3 的子数组的元素总和是:7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。
使用截断式 整数除法,avg[3] = 37 / 7 = 5 。- 中心为下标 4 的子数组,avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
- 中心为下标 5 的子数组,avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
- avg[6]、avg[7] 和 avg[8] 是 -1 ,因为在这几个下标后的元素数量都不足 k 个。
解题思路
class Solution {
public int[] getAverages(int[] nums, int k) {
long sum = 0;
int[] avgs = new int[nums.length];
Arrays.fill(avgs, -1); // 数组填充-1,只有满足条件才会修改数字
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
// 尚未构成有效窗口
if (i < 2 * k) {
continue;
}
avgs[i - k] = (int) (sum / (2 * k + 1)); // 注意是除 2 * k + 1
sum -= nums[i - 2 * k];
}
return avgs;
}
}
2379. 得到 K 个黑块的最少涂色次数
题目描述
给你一个长度为 n 下标从 0 开始的字符串 blocks ,blocks[i] 要么是 'W' 要么是 'B' ,表示第 i 块的颜色。字符 'W' 和 'B' 分别表示白色和黑色。
给你一个整数 k ,表示想要 连续 黑色块的数目。
每一次操作中,你可以选择一个白色块将它 涂成 黑色块。
请你返回至少出现 一次 连续 k 个黑色块的 最少 操作次数。
示例
输入:blocks = "WBBWWBBWBW", k = 7
输出:3
解释:
一种得到 7 个连续黑色块的方法是把第 0 ,3 和 4 个块涂成黑色。
得到 blocks = "BBBBBBBWBW" 。
可以证明无法用少于 3 次操作得到 7 个连续的黑块。
所以我们返回 3 。
解题思路
class Solution {
public int minimumRecolors(String blocks, int k) {
int maxB = 0;
int cur = 0;
// 转换问题为,求长度为k的子串,最多含有B的数量
for (int i = 0; i < blocks.length(); i++) {
cur += blocks.charAt(i) == 'B' ? 1 : 0;
if (i + 1 < k) {
continue;
}
maxB = Math.max(cur, maxB);
if (blocks.charAt(i - k + 1) == 'B') {
cur--;
}
}
return k - maxB;
}
}


评论